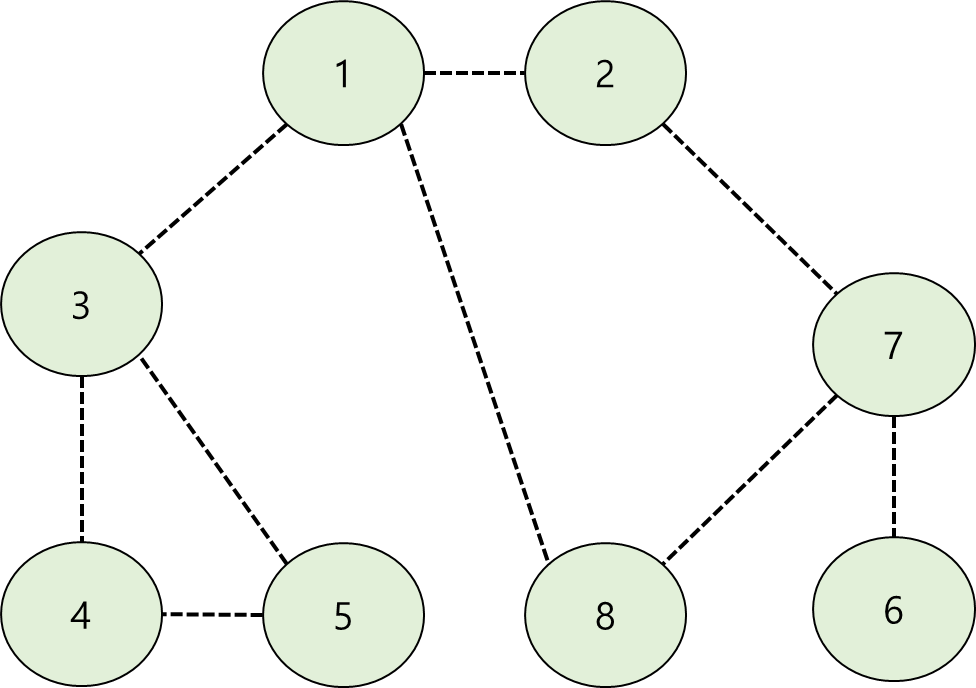
그래프는 노드와 노드를 연결하는 가장자리가 있는 데이터 구조입니다. 철저한 그래프 검색을 위한 기본 알고리즘은 DFS와 BFS입니다.
검색이 가능하려면 먼저 데이터 구조를 정의해야 합니다.
차트는 두 가지 방식으로 제공됩니다.
1. 인접 행렬(2D 배열)
2. 동네 목록(목록)
행렬에는 ‘인덱스’가 있습니다. 인덱스는 랜덤 액세스를 허용하므로 특정 노드에 대한 액세스가 빠릅니다. 하지만 가비지 값을 담고 있는 메모리 공간을 배열 구조로 관리해야 하기 때문에 메모리를 많이 낭비한다.
인접 목록 방법은 목록 데이터 구조를 사용합니다. “연결”형 데이터 구조이기 때문에 주어진 노드에서 시작하여 이웃 노드를 순회할 때 유리합니다. 인접 노드는 “인덱스”가 아닌 “주소”로 액세스하므로 메모리 낭비가 적습니다. 그러나 랜덤 액세스가 아닌 참조로 액세스하기 때문에 검색 속도가 느립니다.
DFS(깊이 우선 탐색): 깊이 우선 탐색
DFS 알고리즘은 스택다음과 같이 구현됩니다.
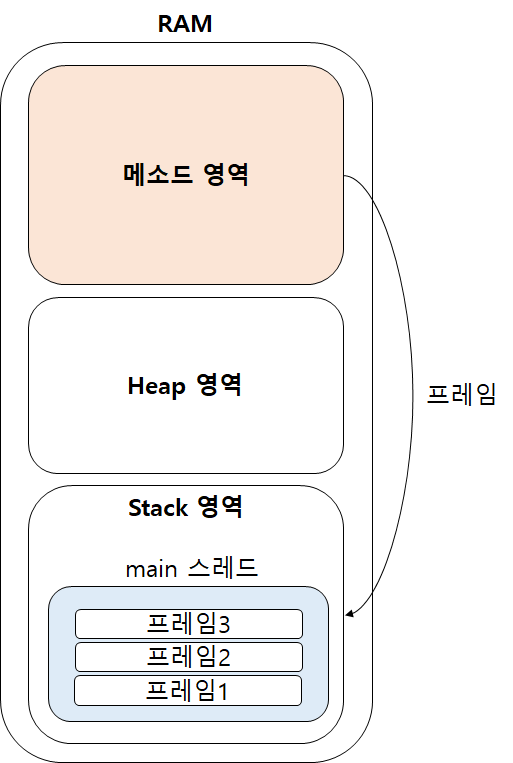
일반적인 메서드를 사용하면 프레임이 호출될 때 스택 영역에 누적됩니다. 따라서 DFS 알고리즘 재귀 호출원리는 간단합니다.
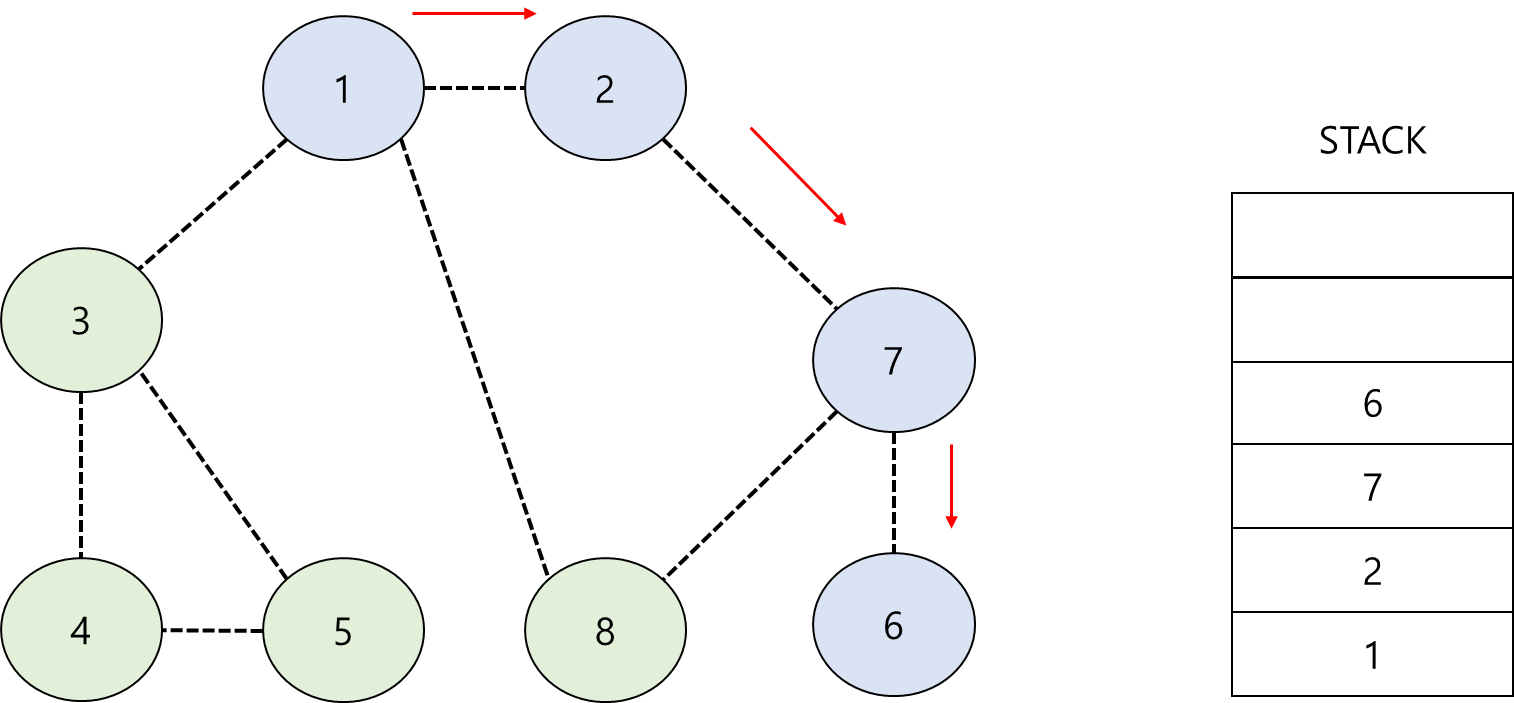
그래프 데이터 구조를 보면 이웃 노드를 방문하면서 쌓(푸시)된다. 그리고 이웃 노드가 없는 노드(6)에 도달하면 해당 노드를 팝(pop)하고 이웃 노드 7을 검색한다.
LiFO(Last In First Out)인 스택은 이전에 방문한 노드 정보를 기억하여 깊이를 “먼저” 검색할 수 있습니다. 다음과 같은 FIFO(First In First Out) 구조 B. 대기열은 이전에 방문한 노드를 기억하지 못하므로 먼저 깊이 탐색할 수 없습니다.
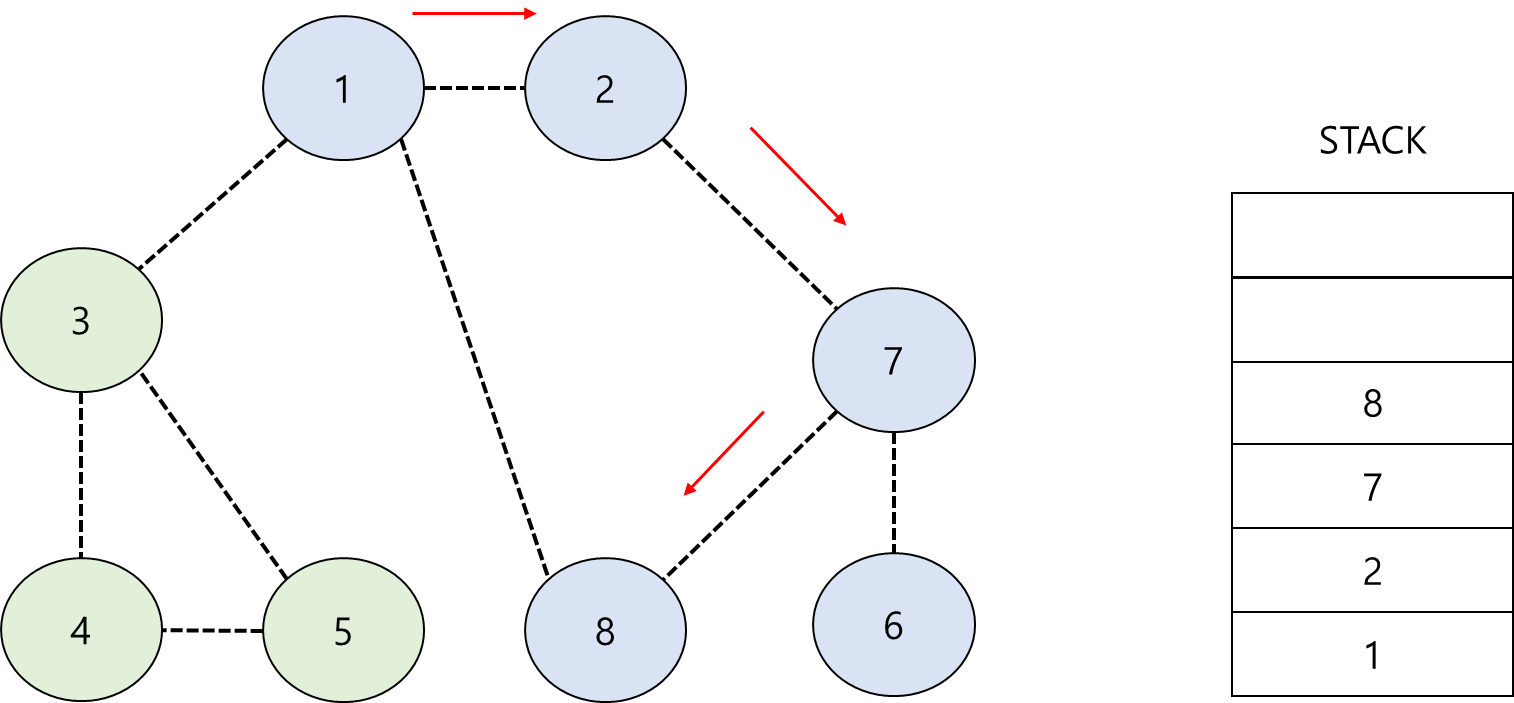
이때 방문기록은 배열을 생성하여 관리한다. 이와 같이 PUSH와 POP을 반복하여 주변 노드를 탐색하면 그래프의 모든 노드를 탐색할 수 있다.
코드 구현
스택 영역의 메모리는 재귀 호출에 사용되므로 별도의 스택 데이터 구조를 만들 필요가 없습니다.
# DFS 함수
def dfs(graph,v,visited):
visited(v) = True #방문처리
print(v,end=' ') #방문노드 출력
for i in graph(v): # 인접노드 순회
if not visited(i): # 방문이력 있는지 체크
dfs(graph,i,visited) # 재귀호출
#Graph 자료구조
graph = (
(),
(2,3,8),
(1,7),
(1,4,5),
(3,5),
(3,4),
(7),
(2,6,8),
(1,7)
)
#방문이력관리 배열
visited = (False)*9
#DFS 함수 호출
dfs(graph,1,visited)
참조
이것은 Python에 참여하기 위한 프로그래밍 테스트입니다.
네이버 도서에 대한 자세한 정보를 제공합니다.
search.shopping.naver.com
