근호를 사용하여 식을 평가할 때 가장 중요한 부분은 분모의 합리화입니다. 이 기사에서는 분모 합리화 방법과 분모 합리화 이유를 요약합니다.
분모 합리화란 무엇입니까?
- 분모의 합리화 : 분모에 근호가 있는 무리수가 있는 경우 분모와 분자에 0이 아닌 같은 수를 곱하면 분모가 유리수로 바뀝니다.
분모를 어떻게 합리화합니까?
방법은 다음과 같습니다.
근호 안에 제곱수가 있으면 제곱근이 사라지는 성질을 이용하다.
분모의 무리수에 분모와 분자를 곱하여 분모를 유리수로 변환합니다.
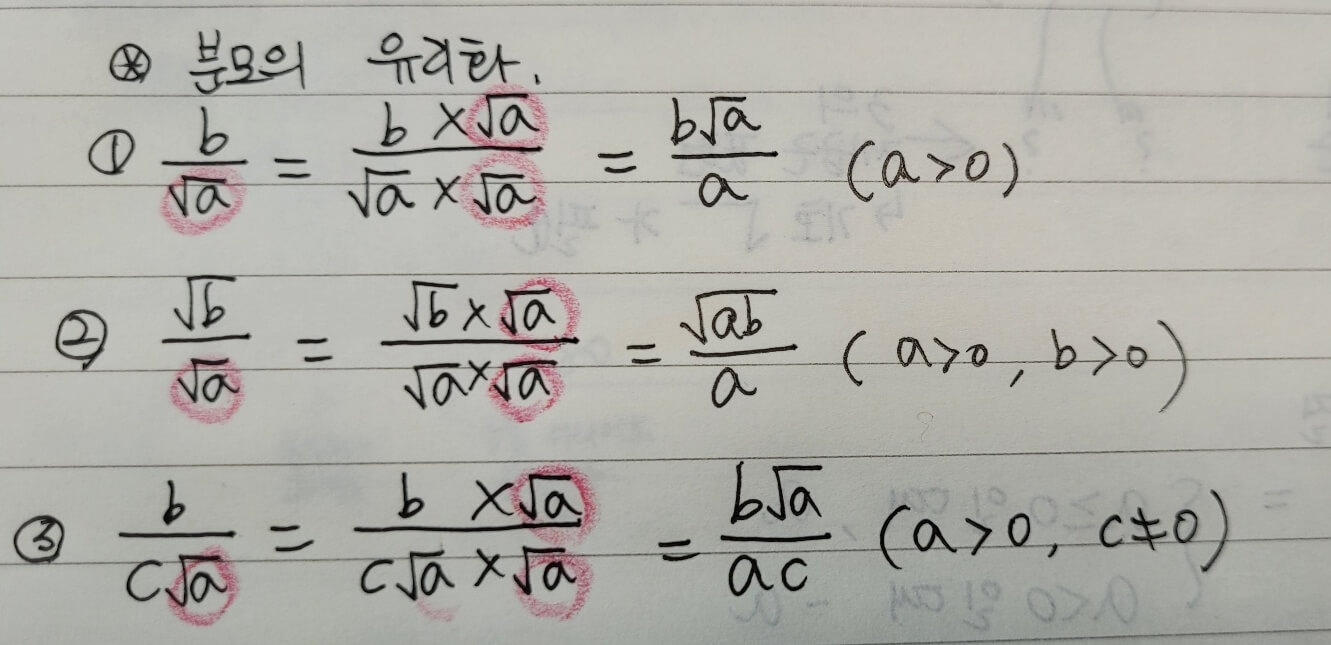
분모를 합리화하는 이유는 무엇입니까?
분모에 무리수가 있으면 계산이 복잡해집니다.
그러나 분모를 유리수로 바꾸면 계산이 쉬워집니다.
예를 들어 보겠습니다.
1/√2=1÷√2=1÷1.414213…으로 계산됩니다.
글레이징을 했다면?
계산은 1/√2=√2/2=1.414213…÷2=0.7071065…로 단순화됩니다.
또한 숫자의 크기도 쉽게 판단할 수 있도록 수직선에 표시됩니다.
분모가 무리수인 두 방정식을 더할 때 분모를 유리수로 변경하면 나누기가 더 쉬워집니다.
즉, 분모를 합리화하는 이유는 계산의 편의를 위함이다.
*공유하기 좋은 글*
무리수와 오류의 의미/특성을 정리해볼까요?